Zadanie
Niektorý KSP-áci1 práve končia magisterské štúdium. Už len tento fakt je celkom šialená jazda. Medzi týmito KSP-ákmi je aj Jaro. Jaro teraz každý večer poctivo trávi na farme (serverovej) a počíta kaktusy. Dáva to zmysel? (Ne)bojte sa, po piatich rokoch vysokej školy bude.
Jaro už má toho všetkého dosť a rozhodol sa, že si pôjde vyvetrať hlavu. Normálny človek by išiel na futbal alebo na kofolu, Jaro sa ale rozhodol, že sa pôjde prevetrať na kolotoč. Ako nástroj svojho plánu si zvolil ruské kolo.
Na zľavomate vyhrabal kupón a už aj stál pred kolotočom. Hneď aj pochopil, prečo bola na tento kolotoč taká veľká zľava. Konštrukciu mal hrdzavú, farbu opadanú, otáčal sa podozrivo rýchlo, a ešte aj kabínky mal povešané kade-tade.
Jaro si teraz musí jednu z týchto kabíniek vybrať.
Jeho mentálne sily sú už ale na dne a chcel by vás poprosiť o pomoc.
Úloha
Celú situáciu si môžeme predstaviť v dvoch rozmeroch (výška a šírka). Každá kabínka sa na začiatku nachádza v nejakom bode roviny. Kolotoč sa otáča rovnomerným otáčavým pohybom okolo stredu, ktorý je v bode \([0,0]\). Jaro by si chcel vybrať kabínku, v ktorej sa bude najdlhšie cítiť nad vecou, t. j. takú, ktorá bude počas jednej otáčky kolotoča najdlhší čas vyššie ako všetky ostatné kabínky. Zistite, ktorá to je!
Formát vstupu
V prvom riadku je číslo \(n\), \((1 \leq n \leq 10^6)\) – počet kabíniek na kolotoči. Nasleduje \(n\) riadkov, \(i\)-ty z nich obsahuje čísla \(x_i\) \(y_i\) (\(-10^5 \leq x_i, y_i \leq 10^5\)) – súradnice \(i\)-tej kabínky. Môžete predpokladať, že žiadne dve kabínky nemajú rovnaké súradnice a všetky súradnice sú celočíselné.
Formát výstupu
Vypíšte súradnice najlepšej kabínky. Ak je takých viac, vyberte tú s najmenšou \(x\)-ovou súradnicou. Ak je aj takých viac, vyberte tú s najmenšou \(y\)-ovou súradnicou.
Hodnotenie
Pre jednotlivé testovacie sady platia nasledujúce obmedzenia:
| číslo sady | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|
| \(n \leq\) | \(10^3\) | \(10^4\) | \(10^5\) | \(10^6\) |
Príklady
Input:
5
-1 -1
1 -1
-1 1
1 1
0 0Output:
-1 -1Na vstupe je štvorec, každá kabínka bude najvyššie štvrtinu času, okrem strednej, ktorá bude vždy v strede.
Input:
8
-1 0
1 0
0 1
0 -4
0 0
1 1
2 2
1 -1Output:
0 -4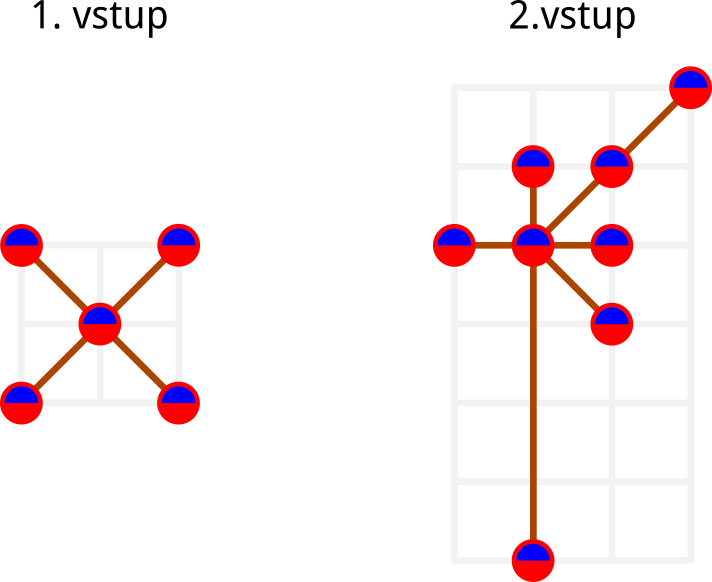
Pred čítaním vzorového riešenia odporúčame prečítať si v KSP Kuchárke články o geometrii, konkrétne článok o skalárnom súčine a článok o konvexnom obale.
Konvexný obal
Prvé pozorovanie potrebné na vyriešenie tejto úlohy je nasledujúce: na to, aby sa mohla kabínka dostať nad všetky ostatné, musí ležať na konvexnom obale všetkých kabíniek. Ak neleží, znamená to, že v každom momente je nad ňou nejaká hrana konvexného obalu. Aspoň jeden koniec tejto hrany je vtedy vyššie ako daná kabínka. Na začiatku si teda môžeme zostrojiť konvexný obal všetkých kabíniek a tie kabínky, ktoré nie sú jeho vrcholmi, môžeme rovno zahodiť.
Najlepší bod
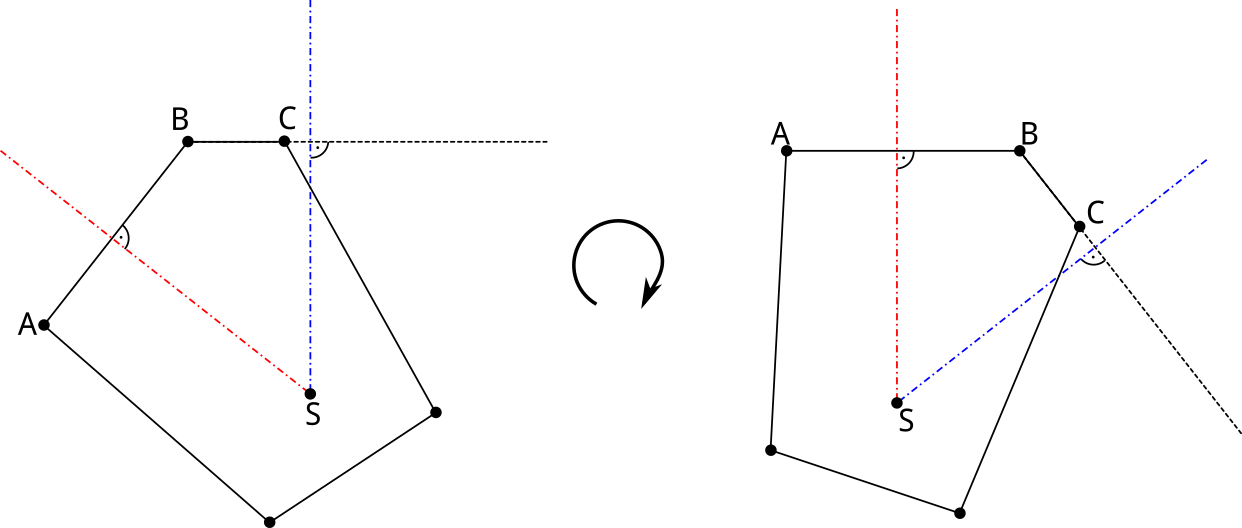
Keď už máme konvexný obal, stačí nám o každom jeho vrchole zistiť, ako dlho bude najvyššie. Vezmime si ľubovoľný vrchol \(B\) z nášho konvexného obalu. Vrchol, ktorý je na obale pred vrcholom \(B\) označme \(A\) a nasledujúci vrchol na obale označme \(C\). Stred, okolo ktorého sa celý kolotoč točí, označme \(S\). Bod \(B\) začína byť najvyššie vtedy, keď je hrana \(BC\) vo vodorovnej polohe, a prestáva vtedy, keď sa do vodorovnej polohy dostane hrana \(AB\). Uhol, o ktorý sa kolotoč otočí medzi týmito dvoma stavmi, je uhol ktorý zvierajú kolmice na tieto strany prechádzajúce bodom \(S\) (na obrázku červená a modrá priamka). Kolotoč sa otáča konštantnou uhlovou rýchlosťou, veľkosť tohto uhla je teda priamo úmerná času, počas ktorého bude bod \(B\) najvyššie. Najlepší je teda bod, ktorý má tento uhol maximálny.
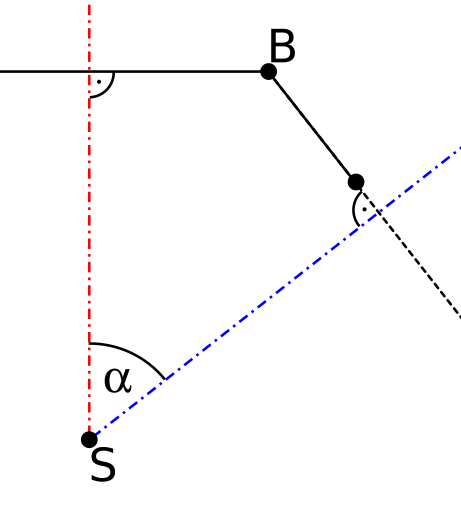
Uhol, ktorý sa snažíme maximalizovať, si označme \(\alpha\). Zo súčtu vnútorných uhlov štvoruholníka na nasledujúcom obrázku vyplýva, že uhol \(|\measuredangle ABC|\) je rovný \(180^\circ - \alpha\). Preto nám stačí nájsť taký vrchol konvexného obalu, pri ktorom je najmenší vnútorný uhol. Vnútorné uhly konvexného mnohouholníka sú vždy menšie než \(180^\circ\). Z toho vyplýva, že veľkosť vnútorného uhla je jednoznačne určená jeho kosínusom. Teraz nám stačí nájsť vrchol, pri ktorom je vnútorný uhol s najväčším kosínusom. A kosínus vnútorného uhla ľahko vyrátame pomocou skalárneho súčinu.
Časová a pamäťová zložitosť
Časová zložitosť výpočtu konvexného obalu je \(O(n\log n)\). Po tomto výpočte už len v lineárnom čase prejdeme body z konvexného obalu a nájdeme najlepší z nich. Pamäťová zložitosť je \(O(n)\).
#include <algorithm>
#include <vector>
#include <iostream>
#include <cmath>
using namespace std;
struct Point {
long long x, y;
bool operator < (Point p){
if(x == p.x)
return(y < p.y);
else
return(x < p.x);
}
Point(long long a, long long b){
x = a;
y = b;
}
Point(){
x = 0;
y = 0;
}
};
// kladné ak sa OAB točí doľava
long long cross(Point O, Point A, Point B){
return (A.x - O.x) * (B.y - O.y) - (A.y - O.y) * (B.x - O.x);
}
// dot product, ktory v sebe skrýva kosínus uhla
long long dot(Point O, Point A, Point B){
return (A.x - O.x) * (B.x - O.x) + (A.y - O.y) * (B.y - O.y);
}
double length(Point O, Point A){
return sqrt(pow(A.x - O.x, 2) + pow(A.y - O.y, 2));
}
bool smallerAngle(int i, int j, vector<Point> &hull){
Point a1 = hull[i-1];
Point c1 = hull[i];
Point b1 = hull[i+1];
Point a2 = hull[j-1];
Point c2 = hull[j];
Point b2 = hull[j+1];
// porovnáme kosínus uhla a1,c1,b1 a a2,c2,b2 (delenie upravíme na násobenie)
// (a1.b1)/(|a1|*|b1|) > (a2.b2)/(|a2|*|b2|)
// (a1.b1)*(|a2|*|b2|) > (a2.b2)*(|a1|*|b1|)
double l = dot(c1, a1, b1) * (length(c2, a2) * length(c2, b2));
double r = dot(c2, a2, b2) * (length(c1, a1) * length(c1, b1));
if(l > r || (l == r && c1 < c2))
return true;
else
return false;
}
// vráti body na konvexnom obale v ľavo točivom smere (prvý bod je rovnaký ako posledný)
vector<Point> convex_hull(vector<Point> &points){
vector<Point> hull;
// zoradíme body od ľava
sort(points.begin(), points.end());
// Dolná časť obalu
for(int i = 0; i < points.size(); i++){
while(hull.size() >= 2 && cross(hull[hull.size()-2], hull[hull.size()-1], points[i]) <= 0)
hull.pop_back();
hull.push_back(points[i]);
}
// horná časť obalu
int z = hull.size() + 1; //začiatok dolnej časti
for(int i = points.size() - 2; i >= 0; i--){ // -2 aby tam nebol krajný bod dva krát
while(hull.size() >= z && cross(hull[hull.size()-2], hull[hull.size()-1], points[i]) <= 0)
hull.pop_back();
hull.push_back(points[i]);
}
return hull;
}
int main(){
int n;
cin >> n;
vector<Point> points;
for(int i = 0; i < n; i++){
long long a, b;
cin >> a >> b;
points.push_back(Point(a, b));
}
if(n == 1){
cout << points[0].x << " " << points[0].y << endl;
return 0;
}
if(n==2){
sort(points.begin(), points.end());
cout << points[0].x << " " << points[0].y << endl;
return 0;
}
vector<Point> hull = convex_hull(points);
hull.push_back(hull[1]);
int where = 1;
for(int i = 1; i < hull.size() - 1; i++)
if(smallerAngle(i, where, hull)) where = i;
cout << hull[where].x << " " << hull[where].y << endl;
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.