Skalárny súčin a vektorový súčin

Predtým ako sa pustíte do čítania tohto článku, odporúčame najprv si pozrieť Úvod do výpočtovej geometrie.

Skalárny súčin

Skalárny súčin (po anglicky dot product) je operácia na dvoch $n$-rozmerných vektoroch. Výsledkom tejto operácie je číslo (čiže skalár, nie vektor).
Skalárny súčin označujeme bodkou. Nech $A = (a_1, \dots, a_n)$ a $B = (b_1, \dots, b_n)$ sú vektory. Potom

$$A \cdot B = a_1 b_1 + a_2 b_2 + \dots + a_n b_n$$

Pre dvojrozmerné vektory je ich skalárny súčin $A\cdot B = a_1b_1 + a_2b_2$.

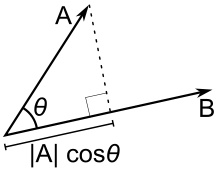
Zároveň, keď $\theta$ je uhol, ktorý zvierajú vektory $A$ a $B$, tak platí

$$A \cdot B = ||A|| \cdot ||B|| \cdot \cos\theta$$

kde $||X||$ označuje dĺžku vektora $X$.

Skalárnym súčinom vieme zisťovať dĺžku vektora ($A\cdot A = ||A||^2$), vieme overovať, či sú dva vektory kolmé (práve vtedy, keď $A\cdot B = 0$) a rozhodovať, či kolineárne vektory (také, ktoré ukazujú rovnakým alebo presne opačným smerom) ukazujú rovnakým alebo opačným smerom (podľa znamienka skalárneho súčinu). Skalárny súčin sa dá využiť aj pri výpočte vzdialenosti bodu od priamky alebo na nájdenie päty kolmice na danú priamku vedúcu cez daný bod.

Napríklad:

• Máme body $X,Y,Z$ ležiace na jednej priamke a máme zistiť, či bod $Z$ leží na úsečke $XY$. Stačí spočítať $w = (X-Z)\cdot(Y-Z)$. Ak nám vyjde záporné $w$, bod $Z$ leží vo vnútri úsečky. Ak kladné, bod leží mimo úsečky. Ak je $w$ nula, $Z$ je totožný s jedným z bodov $X,Y$.

Vektorový súčin

Na rozdiel od skalárneho súčinu, vektorový súčin (po anglicky cross product) je definovaný len v troch rozmeroch. Matematická definícia je:

$$A \times B = (a_1, a_2, a_3) \times (b_1, b_2, b_3) = (a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1)$$

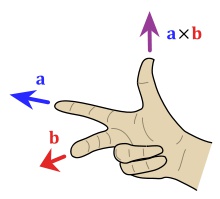
Výsledkom vektorového súčinu je vektor, ktorý je kolmý na oba vektory a jeho dĺžka je rovná obsahu štvoruholníka $((0,0), A, A+B, B)$. Existujú dva opačné vektory s takouto dĺžkou ($A \times B = - B \times A$). Ak chceme zistiť, ktorý z nich je výsledkom súčinu, použijeme pravidlo pravej ruky. Ukazovák ukazuje v smere prvého vektora, prostredník v smere druhého a palec bude ukazovať v smere vektorového súčinu.

Špeciálne ak sú pôvodné vektory lineárne závislé (jeden je násobkom druhého), výsledkom vektorového súčinu je nula (t.j. vektor $(0,0,0)$).

Ak potrebujeme vektorovo vynásobiť dvojrozmerné vektory $A = (a_1, a_2)$ a $B = (b_1, b_2)$, jednoducho vektorovo vynásobíme trojrozmerné vektory $A'$ a $B'$, ktoré majú prvé dve súradnice rovnaké ako $A$ a $B$ a tretiu súradnicu majú nulovú:

$$(a_1, a_2, 0) \times (b_1, b_2, 0) = (0, 0, a_1b_2-a_2b_1)$$

Zaujímavá je orientovaná dĺžka výsledného vektora, čiže $a_1 b_2-a_2 b_1$. Keď hovoríme o vektorovom súčine ako o čísle, máme na mysli práve túto hodnotu: $a_1 b_2-a_2 b_1$.

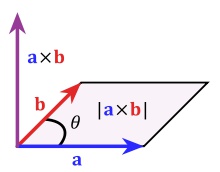
Na čo je teda vektorový súčin dobrý? Opäť ním dokážeme zistiť niečo o uhle medzi vektormi.

$$||A \times B|| = ||A|| \cdot ||B|| \cdot \sin\theta$$

Ak sú vektory kolineárne, výsledok je $0$. Ak je $A$ "naľavo" od $B$, ich vektorový súčin je kladný, a ak je $A$ "napravo" od $B$, je ich vektorový súčin záporný (čiže $A\times B = -B\times A$). Vďaka tomu vieme zisťovať, či daný bod leží na danej priamke, či je bod vo vnútri konvexného $n$-uholníka, či sa dve úsečky pretínajú, či je bod vo vnútri ľubovoľného $n$-uholníka a mnoho ďalších vecí.

Napríklad:

• Máme daný bod $X$ a priamku prechádzajúcu bodmi $YZ$ a máme zistiť, či sa bod nachádza na priamke, naľavo od nej alebo napravo od nej (keď sa pozeráme v smere z $Y$ do $Z$). Spočítame $(Z-Y)\times(X-Y)$. Ak vyjde 0, bod leží na priamke. Ak vyjde kladné číslo, bod $X$ je naľavo, ak vyjde záporné číslo, bod je napravo.

• Máme daný bod $X$ a konvexný $n$-uholník s vrcholmi $Y_1,\dots, Y_n$ a máme zistiť, či je bod vo vnútri $n$-uholníka. $n$-uholník je konvexný, ak má každý jeho vnútorný uhol menej ako $180^{\circ}$. Spočítame $z_i = (Y_{i+1}-Y_i)\times(X-Y_i)$ (pričom $Y_{n+1} = Y_1$). Ak sú všetky hodnoty kladné, alebo všetky záporné, tak je bod $X$ vo vnútri. Ak si predstavíme, že sme predĺžili každú stranu $n$-uholníka na priamku, hodnoty $z_i$ nám hovoria o tom, či je bod od daných priamok napravo alebo naľavo. No a na to, aby sa bod $X$ nachádzal vo vnútri, musí sa nachádzať napravo od každej z priamok, alebo naľavo od každej z nich.

• Máme dané dve úsečky $XY$ a $ZW$ a máme zistiť, či sa pretínajú. Overíme, či úsečka $XY$ pretína priamku $ZW$ a úsečka $ZW$ pretína priamku $XY$. Overenie prvej podmienky spravíme napríklad tak, že sa pozrieme na vektorové súčiny $(X-Z)\times(W-Z)$ a $(Y-Z)\times(W-Z)$. Tieto musia mať opačné znamienka, resp. ich súčin musí byť záporný.

• Máme daný bod $X$ a ľubovoľný $n$-uholník s vrcholmi $Y_1,\dots, Y_n$ a máme zistiť, či je bod vo vnútri $n$-uholníka. Ak je bod $X$ vo vnútri, každá polpriamka, ktorá v ňom začína pretína $n$-uholník nepárny počet krát. Ak je $X$ vonku, tak je počet pretnutí vždy párny. Takže pomocou vektorového súčinu spočítame priesečníky nejakej polpriamky s hranami $n$-uholníka. Treba si však dávať pozor na prípady, kedy vrcholy $n$-uholníka ležia na priamke.

• Máme daný trojuholník pomocou bodov $A$, $B$, $C$ a chceme spočítať jeho obsah. Tu využijeme to, že dvojrozmerné vektory vieme preniesť do trojrozmerného priestoru pridaním nulových súradníc. Potom je výsledok $||(A - C) \times (B - C)||/2$. Špeciálne, keď je jeden z bodov (povedzme $C$) nulovým -- $(0, 0)$, tak výsledok je $|a_1 b_2-a_2 b_1| / 2$.