Lazy propagation (alebo, ak chcete, lenivé šírenie informácie) je technika, pomocou ktorej dokážeme v intervalových stromoch spracúvať požiadavky typu ,,zmeň rovnakým spôsobom všetky prvky z intervalu $[l, r)$'' v čase $O(\log n)$.
Na to, čo všetko sa môže znamenať ,,zmeň rovnakým spôsobom'' sa poriadne pozrieme na konci tohto článku. Dovtedy sa budeme zaoberať jedným konkrétnym prípadom: súčtovým intervalovým stromom s požiadavkou ,,prenásob všetky prvky z intervalu $[l,r)$ hodnotou $v$''. Domyslieť, ako to bude vyzerať v iných prípadoch, už nechávame na čitateľovi.
Ako to funguje
Chceme napísať intervalový strom nad postupnosťou $p_0, p_1, \dots, p_{n-1}$, ktorý bude vedieť spracúvať tieto tri druhy požiadaviek (všetky v čase $O(\log n)$):
- Pre daný index $i$ a hodnotu $v$ zmeň prvok $p_i$ na $v$.
- Pre dané indexy $l, r$ vypočítaj súčet všetkých prvkov s indexami z $[l, r)$, teda hodnotu $p_l + p_{l+1} + \dots + p_{r-1}$.
- Pre dané indexy $l, r$ a hodnotu $v$ prenásob všetky prvky s indexami z $[l, r)$ hodnotou $v$.
Druhú požiadavku implementujeme úplne rovnako ako v texte o obyčajnom intervalovom strome, teda ako rekurzívnu funkciu, ktorú zavoláme do koreňa.
Prvú požiadavku v praxi často ani nebudeme potrebovať, keďže všetky potrebné zmeny budeme často vedieť robiť treťou operáciou. Keď ju však predsa len potrebujeme, implementujeme ju ako rekurzívnu funkciu, ktorú zavoláme do koreňa. Koreň sa pozrie, ktorý z jeho synov má vo svojom podstrome $p_i$ a rekurzívne zavolá funkciu do neho. Ten ju zavolá do jedného zo svojich synov a tak ďalej, až kým sa nezavolá do listu, ktorý zodpovedá prvku $p_i$. Ten si zmení hodnotu na $v$. Pri vynáraní z rekurzie všetkých predkov listu $p_i$ aktualizujeme. Presne takto sme to implementovali v objektovo orientovanej implementácii spomínanej v článku o intervalovom strome.
Naivný prístup k tretej požiadavke
Pozrime sa najprv, ako sa dá tretí druh požiadaviek spracúvať menej efektívnym spôsobom.
Opäť použijeme paralelu s úradníkmi z textu o intervalovom strome. Každý vrchol stromu je teda úradník, ktorý má na starosti nejaký úsek postupnosti $p_0, p_1, \dots, p_{n-1}$ a pamätá si jeho súčet. Každý úradník, okrem listov, má dvoch priamych podriadených -- svojich synov v strome. Každý z podriadených je zodpovedný za jednu polovicu úseku svojho šéfa.
Od každého úradníka teraz budeme chcieť, aby vedel spracúvať požiadavku ,,vynásob hodnoty všetkých prvkov z tvojho úseku, ktoré majú index z intervalu $[l, r)$ hodnotou $v$''. Úradníci, ktorí sa starajú iba o jeden prvok (teda listy nášho stromu) to majú jednoduché: pozrú sa, či jeho index leží v $[l, r)$ a podľa toho ho buď prenásobia $v$-čkom, alebo neurobia nič. Vyššie postavený úradník (teda nie list) to môže riešiť nasledovne:
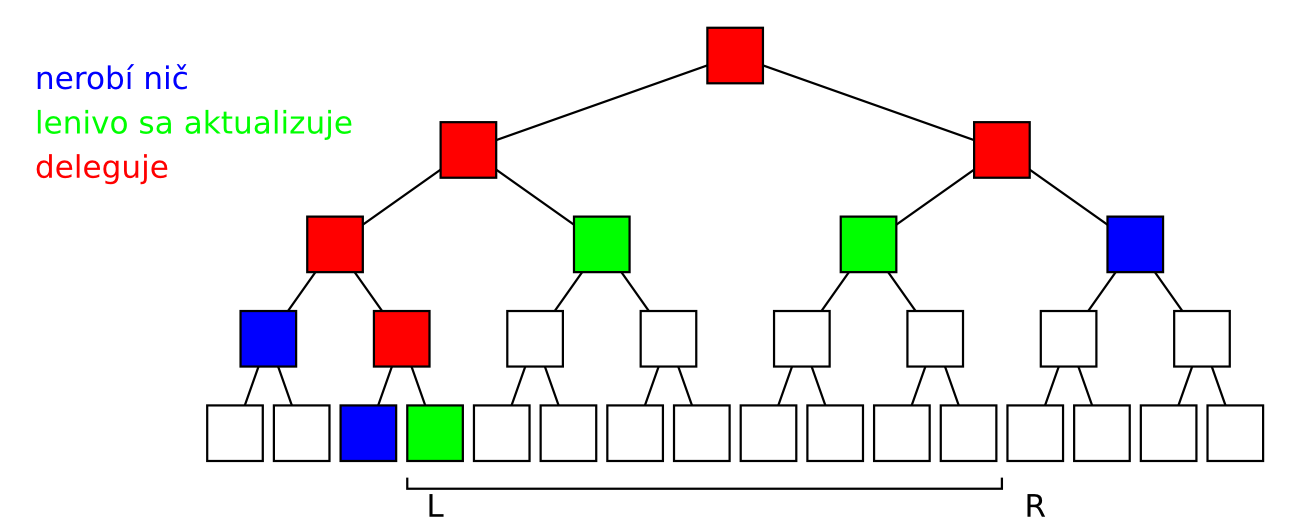
- Ak žiaden z prvkov v mojom úseku neleží v intervale $[l, r)$, nerobím nič.
- Inak delegujem požiadavku na oboch svojich synov. Keď budú hotoví, aktualizujem si svoju hodnotu na súčet ich hodnôt.
Takéto správanie sa dá ľahko implementovať ako rekurzívna funkcia. Keď budeme chcieť prenásobiť prvky z nejakého intervalu nejakou hodnotou, stačí nám túto funkciu zavolať z koreňa. Jediný problém je, že takto napísaná funkcia bude pomalá -- jej časová zložitosť bude $O((r - l) \log n)$, čo pre dlhé intervaly $[l, r)$ bude $O(n)$.
Optimalizácia
Doteraz sme boli zvyknutí, že v listoch intervalového stromu sú uložené prvky $p_0, p_1, \dots, p_{n-1}$ postupnosti, ktorú daný strom reprezentuje a v každom vrchole je súčet prvkov úseku, za ktorý zodpovedá. Po optimalizácii, ktorú sa teraz chystáme spraviť, to už nebude vždy pravda. Niekedy bude v niektorých vrcholoch ,,nesprávna'' hodnota. Bude však platiť, že vždy, keď hodnotu nejakého vrcholu na niečo potrebujeme, bude si tento vrchol pamätať správnu hodnotu.
Všimnime si, že momentálne v našom strome platí nasledovné: Ak niekto od úradníka niečo chce, tak je to jeho šéf, ktorý naňho deleguje nejakú požiadavku. To nám umožní optimalizáciu tretieho druhu požiadaviek. Tá bude založená na lenivosti našich úradníkov.
Občas sa nejakému úradníkovi stane, že mu príde požiadavka tretieho druhu (teda aby prenásobil prvky s indexami z $[l, r)$ hodnotou $v$) pre taký interval $[l, r)$, že celý jeho úsek leží v tomto intervale. Normálne by mal túto požiadavku delegovať na svojich podriadených a potom si aktualizovať svoju hodnotu. Náš úradník je však lenivý a nechce sa mu vstávať zo stoličky, aby mohol dať robotu svojim podriadeným. Preto si svoju prácu trochu uľahčí:
- Ak všetky prvky z jeho úseku prenásobíme hodnotou $v$, aj ich súčet sa zväčší $v$-násobne. Svoju hodnotu si teda náš úradník môže aktualizovať aj sám bez toho, aby si musel zisťovať nové hodnoty svojich podriadených.
- Namiesto toho, aby svojim podriadeným išiel povedať, že si majú všetky svoje prvky prenásobiť hodnotou $v$, si iba do svojho diára napíše poznámku, že by im to niekedy mal povedať.
Podriadení nášho úradníka sa teda nedozvedeli, že si mali zmeniť hodnoty a teraz majú zastaranú informáciu. To nevadí, kým od nich nikto nič nechce. Problém by nastal, keby im niekto dal nejakú požiadavku skôr, než sa ich šéfovi uráči povedať im, že mali zmeniť hodnoty vo svojich úsekoch. Našťastie v našom strome platí, že jediný, kto od nich môže niečo chcieť je ich šéf a ten si na to vie dať pozor:
- Ak úradník v rámci spracúvania nejakej požiadavky potrebuje niečo delegovať na svojich podriadených, najprv sa pozrie do svojeho diára, či im nemal niečo povedať. Ak zistí, že im mal povedať, aby všetky prvky vo svojich úsekoch prenásobili nejakou hodnotou $v$, tak im to najprv povie (a vyškrtne si to z diára) a až keď to spracujú, deleguje na nich robotu, ktorú im chcel dať.
Špecifická situácia nastane, ak od úradníka viackrát po sebe chceme, aby prenásobil všetky prvky svojho úseku nejakým číslom. Pri druhej (a každej ďalšej) takejto požiadavke po sebe si pôjde do diára zapísať, že má povedať svojim synom aby sa prenásobili nejakou hodnotou $v$. Pritom však zistí, že tam už má zapísané, aby im povedal, že sa majú prenásobiť nejakou staršou hodnotou $u$. V takom prípade jednoducho v diári nahradí hodnotu $u$ hodnotou $u \cdot v$, keďže prenásobiť číslo najprv hodnotou $u$ a potom hodnotou $v$ je to isté ako vynásobiť ho hodnotou $u \cdot v$.
Takéto správanie nám zaručí, že vždy, keď od nejakého úradníka niekto niečo potrebuje, tento úradník bude mať aktuálne informácie. Vďaka tomu bude náš strom fungovať korektne napriek tomu, že niektorí úradníci si v niektorých momentoch pamätajú zastaranú informáciu.
Zložitosť
Poďme sa teraz pozrieť na časovú zložitosť jednotlivých požiadaviek.
Vieme, že pri vyhodnocovaní druhej požiadavky voláme rekurzívnu funkciu, ktorá sa postupne zavolá do $O(\log n)$ vrcholov. Pri obyčajnom intervalovom strome v každom z týchto vrcholov urobila (okrem rekurzívnych volaní) $O(1)$ roboty, teda celková zložitosť bola $O(\log n)$.
Teraz sa v každom volaní našej funkcie môže navyše ešte stať, že úradník, do ktorého sme túto funkciu zavolali, potrebuje svojím podriadeným povedať, aby prvky vo svojich úsekoch prenásobili nejakou hodnotou (ktorú mal predtým zapísanú vo svojom diári). To však tiež trvá iba konštantný čas: náš úradník im to povie a oni (keďže sú tiež leniví) to už ďalej rekurzívne nehovoria svojim podriadeným, iba si aktualizujú svoju hodnotu a zapíšu čosi do svojich diárov. Druhá operácia má teda stále časovú zložitosť $O(\log n)$.
S prvým druhom požiadaviek to bude veľmi podobne ako s druhou a tiež budú mať zložitosť $O(\log n)$.
Pri vyhodnocovaní tretieho druhu požiadaviek voláme do koreňa rekurzívnu funkciu. Táto funkcia okrem rekurzívnych volaní robí konštantne veľa práce (úradník musí zistiť, aký prípad nastal, aktualizovať si svoju hodnotu, v niektorých prípadoch zapísať niečo do diára a v iných prípadoch povedať svojim podriadeným aby sa prenásobili číslom, ktoré má v diári). Zložitosť našej funkcie teda bude úmerná počtu vrcholov, na ktoré sa rekurzívne zavolá. Ten však bude presne rovnaký, ako keby sme spracúvali požiadavku druhého druhu pre rovnaký interval -- to, kedy sa funkcia rekurzívne rozvetví, sa riadi na základe rovnakých kritérií.
Preto aj vyhodnocovanie tretieho druhu požiadaviek bude mať zložitosť $O(\log n)$.
Implementácia
Oproti obyčajnému intervalovému stromu potrebujeme urobiť nasledovné zmeny:
- V každom vrchole (okrem listov) si potrebujeme pamätať hodnotu, ktorú má daný úradník v diári (prípadne, že tam nič nemá). To, že úradník nemá v diári žiadnu hodnotu môžeme reprezentovať tak, že tam bude mať hodnotu $1$ -- násobenie jednotkou s prvkami nič nerobí. Pre jednoduchšiu implementáciu môžeme dať diáre aj listom -- budú si do nich občas niečo písať ale aj tak to nikdy nevyužijú. Asymptotickú časovú zložitosť nám to nezhorší.
- Vždy, keď ide nejaký vrchol delegovať robotu na svojich synov, musí si skontrolovať, či má niečo v diári
(a prípadne im o tom dať vedieť). Na tento účel si môžeme implementovať špeciálnu funkciu
nebud_lenivy(). Keďže synovia by si aj tak iba aktualizovali hodnoty a zapísali požiadavku do diára, nemusíme na nich volať funkciu určenú na menenie intervalov, ale hodnoty a diáre im môžeme zmeniť priamo my. - Musíme implementovať funkciu na vyhodnocovanie tretieho druhu požiadaviek. To by malo byť pomerne priamočiare.
class intervalovy_strom
{
class vrchol
{
int hodnota;
int lazy; //hodnota, ktoru budem musiet povedat svojim synom, ked
//sa ich najblizsie budem nieco pytat (teda hodnota, ktoru ma
//uradnik zapisanu v diari)
int zaciatok, koniec; //zaciatok a koniec mojho intervalu
vrchol *lavy, *pravy; //smerniky na synov
public:
//konstruktor. Vytvori vrchol zodpovedajuci intervalu
//[zac, kon) aj s celym podstromom
vrchol(int zac, int kon) : zaciatok(zac), koniec(kon)
{
hodnota = 0;
lazy = 1;
if(koniec - zaciatok > 1)
{
int stred = (zaciatok + koniec)/2;
lavy = new vrchol(zaciatok, stred);
pravy = new vrchol(stred, koniec);
}
else
{
lavy = pravy = NULL;
}
}
//metoda, ktora synom posunie poziadavky, ktore im mali prist uz skor
//ale bol som lenivy
void nebud_lenivy()
{
if(lazy != 1)
{
lavy->lazy *= lazy;
lavy->hodnota *= lazy;
pravy->lazy *= lazy;
pravy->hodnota *= lazy;
lazy = 1;
}
}
//prvy druh poziadavky
void zmen(int i, int h)
{
if(zaciatok == i && koniec == i+1)
{
hodnota = h;
return;
}
nebud_lenivy();
int stred = (zaciatok + koniec)/2;
if(i < stred) lavy -> zmen(i, h);
else pravy->zmen(i, h);
hodnota = lavy->hodnota + pravy->hodnota;
}
//druhy druh poziadavky
int sucet(int l, int r)
{
if(l >= koniec || r <= zaciatok) return 0;
if(l <= zaciatok && r >= koniec) return hodnota;
nebud_lenivy();
return lavy->sucet(l, r) + pravy->sucet(l, r);
}
//treti druh poziadavky
void zmen_interval(int l, int r, int v)
{
if(l >= koniec || r <= zaciatok) return;
if(l <= zaciatok && r >= koniec)
{
lazy *= v; //toto bude fungovat, aj s prazdnym diarom
hodnota *= v;
return;
}
nebud_lenivy();
lavy->zmen_interval(l, r, v);
pravy->zmen_interval(l, r, v);
hodnota = lavy->hodnota + pravy->hodnota;
}
~vrchol() //destruktor
{
if(lavy != NULL) delete lavy;
if(pravy != NULL) delete pravy;
}
};
vrchol *koren;
public:
intervalovy_strom(int velkost)
{
int n = 1;
while(n < velkost) n *= 2; //najdeme najblizsiu vacsiu mocninu dvojky
koren = new vrchol(0, n);
}
void zmen(int i, int h)
{
koren->zmen(i, h);
}
int sucet(int l, int r)
{
return koren->sucet(l, r);
}
void zmen_interval(int l, int r, int v)
{
koren->zmen_interval(l, r, v);
}
~intervalovy_strom()
{
delete koren;
}
};Aké zmeny vieme robiť
Pozrime sa teraz bližšie na to, akými rôznymi spôsobmi môžeme meniť prvky v treťom druhu požiadaviek. Na to budeme potrebovať niektoré veci trochu formálnejšie pooznačovať.
Prvky postupnosti, ktorú náš strom reprezentuje, budeme naďalej volať $p_0, p_1, \dots, p_{n-1}$. Operáciu, ktorú tento strom počíta označme všeobecne ako $\circ$. V prípade súčtového stromu teda symbol $\circ$ bude znamenať $+$, v prípade súčinového bude znamenať $\cdot$ (krát), v prípade maximového bude znamenať binárne maximum (teda operáciu, ktorá vráti väčšie z dvoch čísel). Náš strom teda dokáže pre zadaný interval $[l, r)$ v logaritmickom čase vypočítať hodnotu $$p_l \circ p_{l+1} \circ p_{l+2} \circ \dots \circ p_{r-1} \text{.}$$
Zmenu, ktorú robíme s prvkami v treťom druhu požiadaviek definujeme formálne pomocou ďalšej binárnej operácie $*$ (ktorá môže byť aj rovnaká ako $\circ$). Tretí druh požiadavky teda bude vyzerať nasledovne:
- Pre dané indexy $l, r$ a hodnotu $v$ zmeň každý prvok $p_i$ s indexom $i$ z intervalu $[l, r)$ na $p_i * v$.
V prípade, ktorý sme popisovali v tomto texte, teda oparácia $\circ$ bola $+$ (sčítanie) a operácia $*$ bola $\cdot$ (násobenie).
Na to, aby sme mohli napísať intervalový strom s lenivým šírením pre nejaké dve operácie $\circ$ a $*$, musia platiť nasledovné veci:
- Operácia $\circ$ musí byť asociatívna a pre dané $x, y$ musíme vedieť v konštantnom čase vypočítať $x \circ y$. Táto podmienka musí platiť, aby bolo vôbec možné napísať $\circ$-ový intervalový strom (aj bez lenivého šírenia).
- Ak poznáme hodnoty $l, r, v$ a hodnotu $p_l \circ p_{l+1} \circ p_{l+2} \circ \dots \circ p_{r-1}$, vieme v konštantnom čase vypočítať hodnotu $(p_l * v) \circ (p_{l+1} *v) \circ (p_{l+2} * v) \circ \dots \circ (p_{r-1} * v)$. Toto musí platiť, aby leniví úradníci vedeli aktualizovať svoju hodnotu aj bez toho, aby museli svojim podriadeným hovoriť, že majú zmeniť hodnoty prvkov vo svojich úsekoch.
- Ak poznáme hodnoty $v_1$ a $v_2$, potom vieme v konštantnom čase vypočítať hodnotu $v_3$ takú, že $(x * v_1) * v_2 = x * v_3$ pre každú možnú hodnotu $x$. Toto potrebujeme, aby si leniví úradníci vedeli zmeniť hodnotu vo svojom diári, keď im príde tesne po sebe viacero požiadaviek na zmenu celého ich úseku.
Pre získanie lepšej predstavy sa teraz pozrime na niekoľko konkrétnych príkladov operácií $\circ$ a $*$:
- V súčtovom intervalovom strome (teda keď $\circ$ je $+$) môžeme za operáciu $*$ zobrať napríklad
- sčítanie (budeme vedieť spracúvať požiadavky typu ,,pripočítaj $v$ ku všetkým prvkom s indexami z intervalu $[l, r)$'')
- násobenie (,,vynásob všetky prvky z intervalu $[l, r)$ hodnotou $v$'')
- operáciu ,,vráť druhý prvok'' (teda operáciu $*$ definovanú ako $x * y = y$). To nám v strome umožní spracúvať požiadavky typu ,,zmeň všetky prvky z intervalu [l, r) na hodnotu $v$''.
- V maximovom intervalovom strome môžeme za operáciu $*$ zobrať napríklad
- sčítanie
- násobenie kladným číslom
- ,,vráť druhý prvok''
- binárne maximum (to nám umožní požiadavky typu ,,všetky prvky z intervalu $[l, r)$ menšie ako $v$ zmeň na $v$'').
- binárne minimum
Čas poslednej úpravy: 8. júl 2018 20:46